「トポロジカル相」を鍵とする新しい分野の開拓
トポロジカル相とは、トポロジーとよばれる数学によって特徴づけられる物質相です。トポロジカル物質の最大の特徴は、表面の金属的振る舞いが物質内部の非自明なトポロジーに由来して現れることにあります。例えば、図は量子スピンホール絶縁体と呼ばれる系を表していて、物質内部は絶縁体であるにもかかわらずその端にはスピン流が流れる様子を示しています。興味深いことに、トポロジカル物質の性質は数学的には指数定理を用いて説明され、高エネルギー物理ともアノマリーを通じて関連しているのです。本新学術領域A01班においては、物性物理、高エネルギー物理、数学の3つの分野を融合し、新しい物理を創出することを目的に研究を行っています。
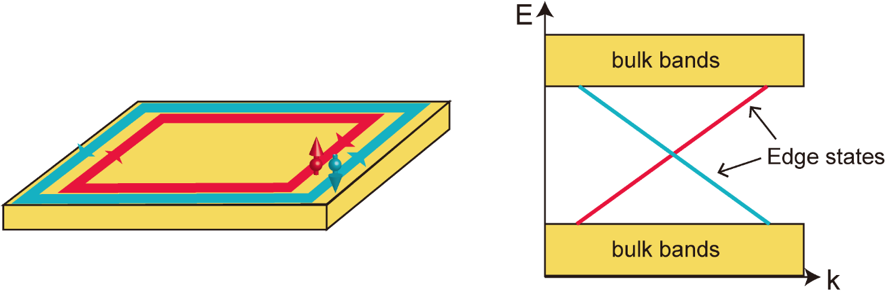
量子スピンホール系のスピン流およびそのバンド構造
APS指数定理とドメインウォールフェルミオン
Atiyah-Patodi-Singerの指数定理は幾何学者の日常の道具です。この研究では、APS指数定理の物理的導出に数学的基礎を与えました。これは、物理から数学への逆輸入になっていて、物理学者三人と数学者三人の共同研究の結晶です。
凝縮系物理での課題の一つにSPT相のバルクエッジ対応があり、その対応の背後の時間反転対称アノマリーの相殺をAPS指数定理が保証することがWittenらにより洞察されました。しかし、その使われ方は間接的であったため、APS指数定理そのものの物理的導出が待たれていました。それを解決したのが論文[1]で、ドメインウォールフェルミオンが物理とAPS指数定理を結ぶ鍵でした。当然、次は、ドメインウォールフェルミオンに数学的基礎を与えねばなりません! それを解決したのが本論文[2]なのです。
[1] H. Fukaya, T. Onogi, and S. Yamaguchi, Physical Review D 96, 125004 (2017).
[2] H. Fukaya, M. Furuta, S. Matsuo, S. Onogi, S. Yamaguchi, and M. Yamashita, "The Atiyah-Patodi-Singer index and domain-wall fermion Dirac operators", preprint.
新奇な高次トポロジカル相の理論的予言
高次トポロジカル相とは、従来のトポロジカル相とは異なって、コーナーやヒンジにトポロジカルに守られた状態をもつ量子相です。本研究は、ある種の指数理論を用いてコーナー状態やヒンジ状態に関連したトポロジーの定義を与えることで、3次元class Aおよび2次元class AIIIの系において高次トポロジカル絶縁体が実現できることを明らかにしました[1,2]。さらに、2次元class AIIIの高次トポロジカル絶縁体のアイデアは3次元の高次トポロジカル相にも拡張されました[3]。本研究は、これらの高次トポロジカル相の構築方法も与えていて、高次トポロジカル相を発見するための新たな指針になると期待されます。
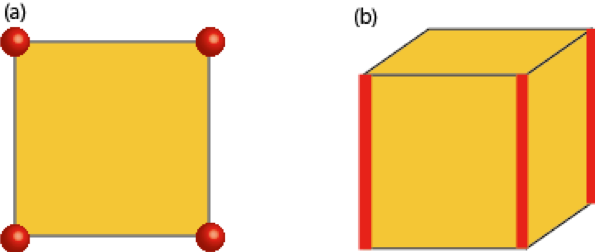
(a) 2次元系におけるトポロジカルコーナー状態。(b) 3次元系におけるヒンジ状態。
[1] S. Hayashi, Comm. Math. Phys. 364(1), 343—356 (2018).
[2] S. Hayashi, Lett. Math. Phys. 109, 2223 (2019).
[3] R. Okugawa, S. Hayashi, and T. Nakanishi, Phys. Rev. B 100, 235302 (2019)
高分子材料のネットワーク構造と数学
この研究では、結び目理論と関連の強い3次元トポロジーの視点から、物質のネットワーク構造を解析します。例えばブロックコポリマーのミクロ相分離構造からネットワークの構造を取り出し、その特徴付けや、その動的な変化の様子を記述します。これらの問題に取り組むためには、新しい数学の理論と新しいシミュレーション方法の構築が必要になることが明らかになりました。これらの理論的な側面の発展と、それを応用することによる新奇材料の開発の両方を連携して進めて行くことを目指しています。

ブロックコポリマーによる3相共連続構造のモデル
ネットワークと共連続構造
ブロックコポリマーのミクロ相分離構造のうち、多相共連続構造に着目し研究を行っています。共連続構造の数学的モデルである3次元空間に埋め込まれた分岐曲面と、絡み合うネットワークの対応を与えました[1]。また、ペプチドと金属イオンが作る絡み目について、12交点の4成分絡み目の2つの構成法についての議論を行いました[2]。

多相共連続構造の数学モデルである分岐曲面
[1] K. Ishihara, Y. Koda, M. Ozawa, and K. Shimokawa, Topology Appl. 257 (2019) 11-21.
[2] T. Sawada, A. Saito, K. Tamiya, K. Shimokawa, Y. Hisada, and M. Fujita, Nature Communications 10, Article number: 921 (2019).
ネットワーク型熱可塑性エラストマーの弾性挙動解析
ハードセグメントとソフトセグメントからなる熱可塑性エラストマー(TPE)は、ミクロ相分離により生成するハードドメインが物理架橋として作用しゴム弾性を発現します。今回自己無撞着場計算と粗視化分子動力学との階層的シミュレーションにより、ダブルジャイロイド(DG)構造を持つTPEの弾性挙動解析を実施しました[1]。通常のTPEの持つ海島構造と異なり、DG構造を形成するTPEはハードドメインが連続構造を持ち、実験的に観察される大きな初期弾性率とその後のしなやかな伸長がシミュレーションにおいても再現されました。さらに応力挙動のブリッジ分率依存性が極めて少ないことも明らかになり、ネットワーク構造特有のメカニズムに基づいた材料設計が期待されます。

ダブルジャイロイド型熱可塑性エラストマーの伸長挙動
[1] T. Aoyagi and S. Yamanaka, in preparation.
炭素材料 – 3次元から2次元、そしてまた3次元へ
物理の視点から見ると、我々の身の回りのほとんどの物質は3次元構造を持っています。1枚の紙でさえ何百万もの原子層の厚さがあるのです。しかし、ほんの2~3原子層の厚さしかない物質もいくつかあります。その代表的な例が「グラフェン」です。グラフェンはダイヤモンドやグラファイト(黒鉛)と同じく、炭素だけからできています。炭素はあらゆる生き物にとって最も大きな割合を占める元素です。そのグラフェンは炭素たった1原子分の厚みからなる原子層でできており、原子レベルで平らな2次元シートです。この2次元シートはいくつかの異常な性質を生み出し、例えば、とても薄いのに象を持ちあげられるほど機械的な強度が高く、どんな金属よりも電気や熱をよく通すことが知られています。グラフェンを世界で最初に作り出したAndre Geim 教授と Konstantin Novoselov教授は2010年のノーベル賞を受賞し、その後、グラフェンのような2次元物質の存在は多くの物理学者や材料科学者に多くのインスピレーションを与え続けています。
現在では、ディスプレイ、高性能な畜電池、金属を使用しない新しい触媒、エネルギー効率の良いコンピュータから優れたフィルターまで、グラフェンには多くの応用が考えられています。しかし、化学的、機械的安定性や良好な電気的特性を持つ一方で、その2次元シート構造が応用上の問題となることがあります。例えば、触媒として使う際には化学反応に関与する表面積をできるだけ大きくしたいのです。このため「3次元構造を持つグラフェン」を作れるのかどうかは、材料科学者にとって興味深い課題です。機械的・電気的な性質を保持するために原子スケールで平坦でありながら、体積当たりの表面積を増やすために3次元的に折り曲げることが必要です。
そのような物質のデザイン手法の開発やそこに現れる性質の解明が我々の研究プロジェクトの目標です。一方では、これは材料科学者の側に多大な労力を要請します。つまり、物質を作った上で、その性質を制御したり測定したりしなくてはならないからです。筑波大学の伊藤准教授らは、炭素でできたスポンジのような3次元構造物であるナノ多孔質グラフェンの作製に非常に大きな進展をもたらしてきました[1-3]。他方では、次世代の材料を生み出すためにどのような構造を作製すべきかを知る必要もあります。そこで、数学と材料科学の密接な協働が極めて重要になります。物質の作製や複雑な計算機シミュレーションはどちらも時間やお金がかかり、トライ&エラーが避けられないことが多く、シンプルでありながらも目標物質の性質を予測できる数学的モデルを構築し、構造情報を機能に結びつける基本原理の理解が不可欠なのです。
数学と材料科学とが交わる具体例のひとつが、炭素原子が作るネットワークのデザインと曲率との関係です。通常、曲率とはなめらかな表面が持つ特徴で、間近で見たときにある表面が平坦な表面からどのくらい曲がっているかを教えてくれます。3次元の炭素ネットワーク中にある炭素原子たちは、多角形で構成される離散表面を形成します(図1左)。そのような表面はなめらかでなく、折れ曲りや角があって通常の定義での曲率は適用できません。この離散表面における曲率の適切な定義が、最近、小谷教授・内藤教授らによって与えられました[4,5]。驚くべきことに、平たい部分が負のガウス曲率を持つ部分(図1左の青色の点で示す)でつながった3次元の炭素構造は無数に構築できます。そのような構造は空間的に周期性があり、紛れもなく結晶性の炭素構造です。局所的には2次元でグラフェンに似ているという点で、これらの構造はダイヤモンドやグラファイトとは異なります。しかし、6角形だけでできた理想的に平坦なグラフェンとは対照的に、サッカーボールのように曲がった構造を実現するために5角形や7角形、8角形の存在が幾何学的に要求されます。
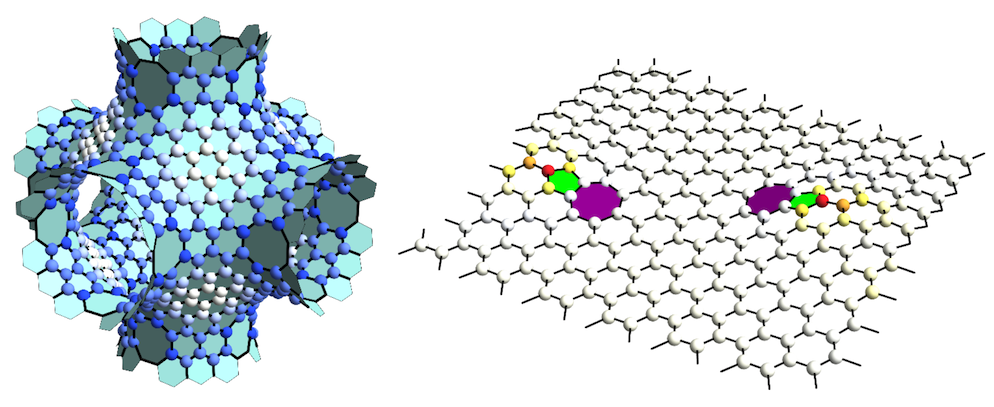
右:5-7欠陥のペアを持つグラフェンシート。ここでも球の色は白(平坦)から赤(正)までのガウス曲率を示す。
曲率と物性とのつながりは伊藤研究室で調べられていて、ナノ多孔質グラフェン構造では曲率が大きな部分の幾何学的安定性が低いことがわかっています。平坦なグラフェンのエネルギーが最も低い(安定性が高い)ため、ナノ細孔グラフェンは平坦になろうとします。しかし、炭素原子は3次元的に連結されているためネットワークの大きな再構成が必要となり、実際に平坦になることはできません。この曲率が大きな場所での幾何学的安定性の低下は、実際にはとても有用となります。そのような箇所では、窒素やリンといった他の種類の原子を導入しやすくなり、例えば半導体を作るために電気的性質を制御することがより簡単なのです。これは、材料の幾何学的な形を設計すれば、その化学的、電気的な性質に影響を与えられること示しています。
この仮説を検証するため、となり合う2つの6角形を5角形と7角形のペアで置き換えた欠陥2つによって曲げられた、ほぼ平坦なグラフェンシートの数値計算を行いました(図1右の緑と紫)。実際、曲率の大きな場所の近くでは、炭素原子を窒素原子で置換するのに必要なエネルギーが平坦な場所よりも著しく低くなっています。こうした欠陥は化学元素のドーピングや触媒反応サイトのホストとして役立ちます。この結果は将来的な応用にとって非常に有望で、グラフェンを3次元物質として形作るだけでなく、その性質を制御するために幾何学的な特徴を積極的に活用できるのです。
この例が示すように、数学と材料科学の協力には2つの方法があります。数学的な概念が物性を理解し予測する助けとなりうる一方、材料科学は数学における新しい問いや視点を見出す着想を与えうるのです。
[1] Y. Ito, Y. Tanabe, H.-J. Qiu, K. Sugawara, S. Heguri, N. H. Tu, K. K. Huynh, T. Fujita, T. Takahashi, K. Tanigaki, and M. Chen, Angewandte Chemie International Edition 53, 4822 (2014).
[2] L. Chen, J. Han, Y. Ito, T. Fujita, G. Huang, K. Hu, A. Hirata, K. Watanabe, and M. Chen, Angewandte Chemie International Edition 57, 13302 (2018).
[3] K. Ji, J. Han, A. Hirata, T. Fujita, Y. Shen, S. Ning, P. Liu, H. Kashani, Y. Tian, Y. Ito, J.-i. Fujita, and Y. Oyama, Nature Communications 10, 275 (2019).
[4] M. Kotani, H. Naito, and T. Omori, Computer Aided Geometric Design 58, 24 (2017).
[5] M. Kotani, H. Naito, and C. Tao, arXiv e-prints, arXiv:1806.03531 (2018).
データ科学が加速する離散幾何学-材料科学連携
複雑ネットワーク解析に基づく物質・材料探索
物質・材料が持つ多様で複雑な構造をネットワークとして抽象化し、複雑ネットワーク科学とデータ科学の視点で解析することで、構造と機能の関係性の解明を目指しています。研究対象としてネットワークポリマーに注目し、複雑ネットワーク指標を用いて架橋高分子のネットワーク構造を定量化することで、構造と力学物性との相関を解析しています。ネットワークから仮想的にリンク(高分子鎖)をランダムに除去していった際のネットワーク構造全体の変化を調べることで、ネットワーク上のパーコレーションを用いて伸長破壊による物質・材料の脆弱性・頑強性も解析しています。また、分子・化合物の複雑な構造を解析するための高性能なグラフ表現手法についても検討しています。
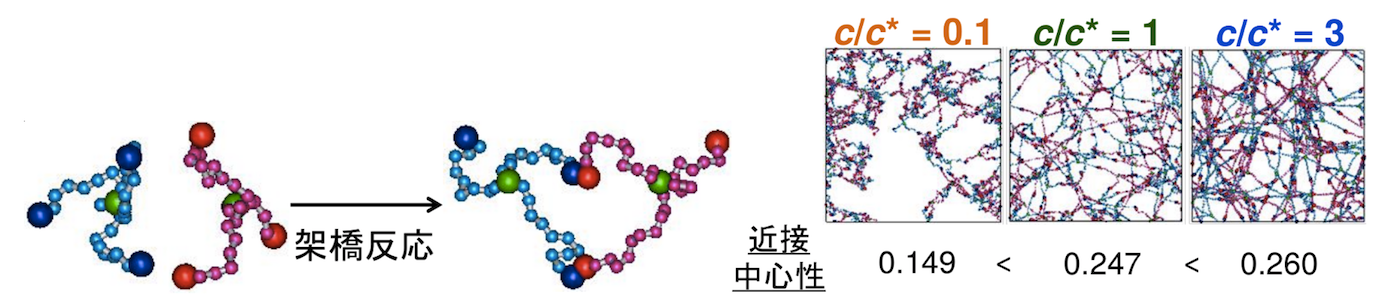
[1](A02-1,A02,B01との連携)複雑ネットワーク指標を用いたネットワークポリマーの構造物性解析
[2](A02-2との連携)粗視化分子動力学シミュレーションで作成した高分子材料の相分離構造解析
[3](A02,B01との連携)ネットワークポリマーの物理系モデル,グラフ構造で特徴づけられる量子系のハミルトニアンとの関連性
[4]【総括班との連携】様々なネットワーク構造を持つ高分子材料の実験データ解析
材料観察画像からの機能推定
機械学習(人工知能)や計算機科学の力を利用して、物質の特性を予測したり計測を簡略化したりする技術を開発しています。具体的には、①ニューラルネットワークを使ってカーボンナノチューブに混ぜた分子の種類を顕微鏡画像から推定する、②シミュレーションによって得られたポリマーの構造から硬さを推定する(図1)、③人の目では計測データからの判別が難しかったトポロジカル超伝導状態の存在有無を推定する、④金属ナノクラスタに少量の電子線を照射するだけで3次元画像を構成する、といったことを行っています。また、「情報科学を利用する」研究だけでなく「情報科学を作る」研究として、機械学習などで頻繁に用いられる確率勾配法という手法の高速化や、その量子版である量子アニーリングの研究にも取り組んでいます。
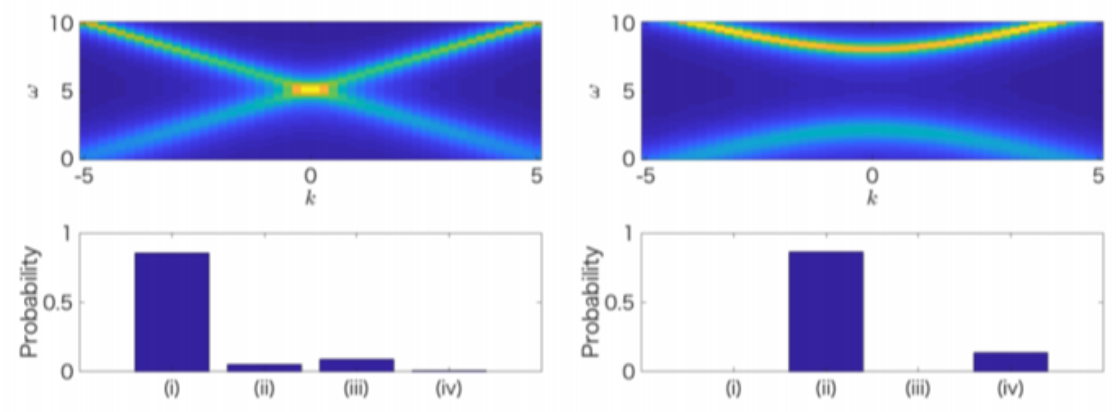
ベイズ推定によるトポロジカル超伝導の判定
[1](A01との連携)徳田悟,相馬清吾,高橋隆,佐藤宇史,中西毅,「ARPESに対するセミパラメトリックベイズ的スペクトル分解」日本物理学会2019年秋季大会(岐阜大学)
[2](A02との連携)A. Ichiki, “Laplacian eigenvalue problem: macroscopic and microscopic energetics for soft matter”, Polymer and networks via topology and entanglement, Aug. 7, 2019, Tokyo, Japan.
[3](A03との連携)一木輝久,「空間分割とラプラス固有値問題」,離散幾何解析とその周辺2018,2019年1月16日(CIC東京)
