Purpose of the Research Project
Creating materials with outstanding functions supports our affluent life and can change our lifestyles and values. Japan has been a world leader in materials science and industry. Creation of new materials, however, has been achieved through a continuous process of trial and error. Researchers and developers utilize both their experience and intuition, but it often takes two or three decades.
Countries like the US, Germany and China, among others, have launched major data-driven materials design projects applying information science. (e.g. Materials Genome Initiative). Computers use findings for search and classifying and material structures are screened for functional materials. But relying on information science alone has its limit because materials structures and function correlations are complex, multiscale and involve multiphysics.
To get meaning from masses of data, scientists must organize information with “good descriptors” that stimulate the imagination. They need a foundation for actualizing and validating material design in order to describe layered structures intuitively and uncover the key principle that connects structure, function and process.
In this context, we propose a universal and mathematical materials science through the collaboration of two disciplines where Japan excels: mathematics and materials science.
Content of the Research Project
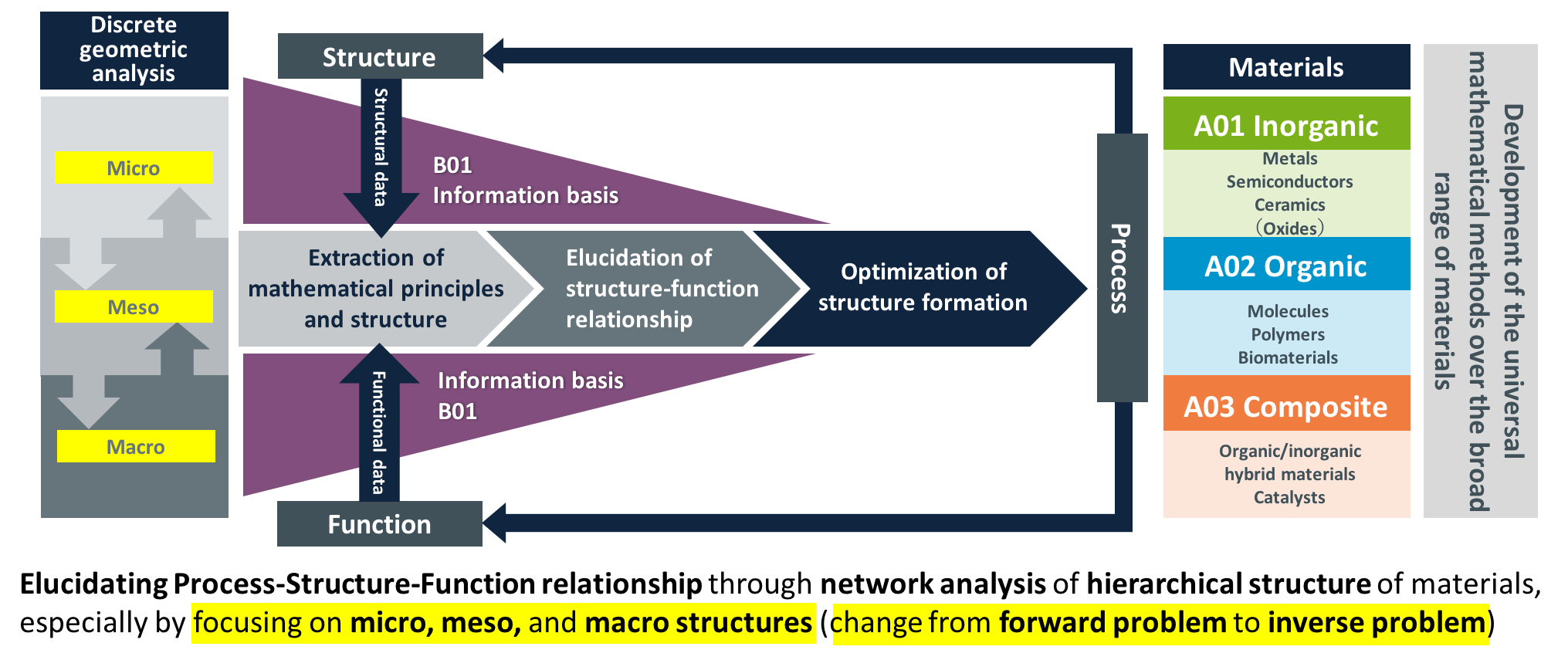
The aim is to understand the key principle that connects structure, function and process of material design and develop the geometric methods. We apply the latest findings in discrete geometric analysis to disordered systems and multilayered hierarchical systems in order to a) clarify micro/mesoscopic structure and macroscopic property relationships and b) change the framework of materials development from a “forward problem (given structure → prediction of properties)” to an “inverse problem (required property → possible structures)”. We use discrete geometric analysis connecting discrete and continuous to find the structures hidden behind the diversity and build a foundation for the unified understanding of complex materials.
We work on the following research based on collaboration between mathematics and materials science.
- A01 Topological Materials (Inorganic)
- A02 Polymeric Materials using Network Analysis (Organic)
- A03 Dynamic Structure Formation of Minimal Surfaces and Nano-structures (Composite)
- B01 Information Science for Materials Science
In particular, we use discrete geometric analysis to expand the unified theory from ordered to disordered systems (random and complex) and from static control to dynamic control.
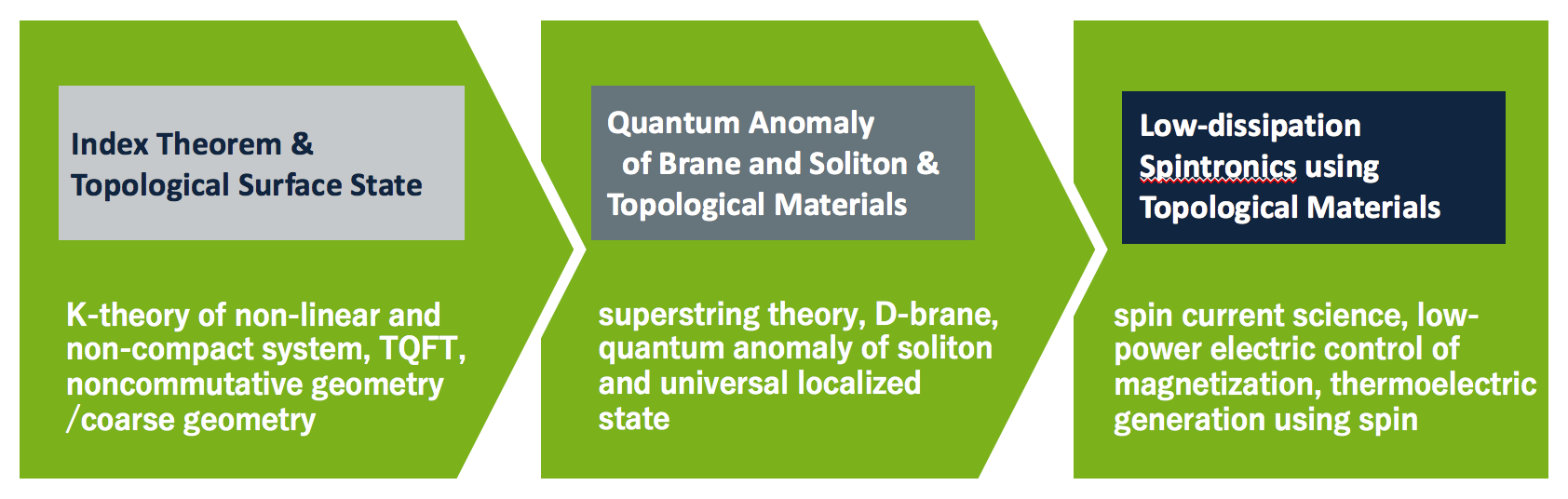
A01 Topological Materials
| Members |
Mikio Furuta (University of Tokyo) Koji Hashimoto (Osaka University) |
|---|---|
| Goal | Elucidating the universal principles how the robust state related with surface topological phase is induced by symmetry breaking. Proposing spintronics devices by creation of novel topological materials. Expanding the theory for ordered systems to non-compact, non-linear, disordered systems. |
| Materials | Topological Materials (low-dissipation device, thermoelectric conversion materials) |
| Mathematical Method | Index Theorem, Superstring Theory |
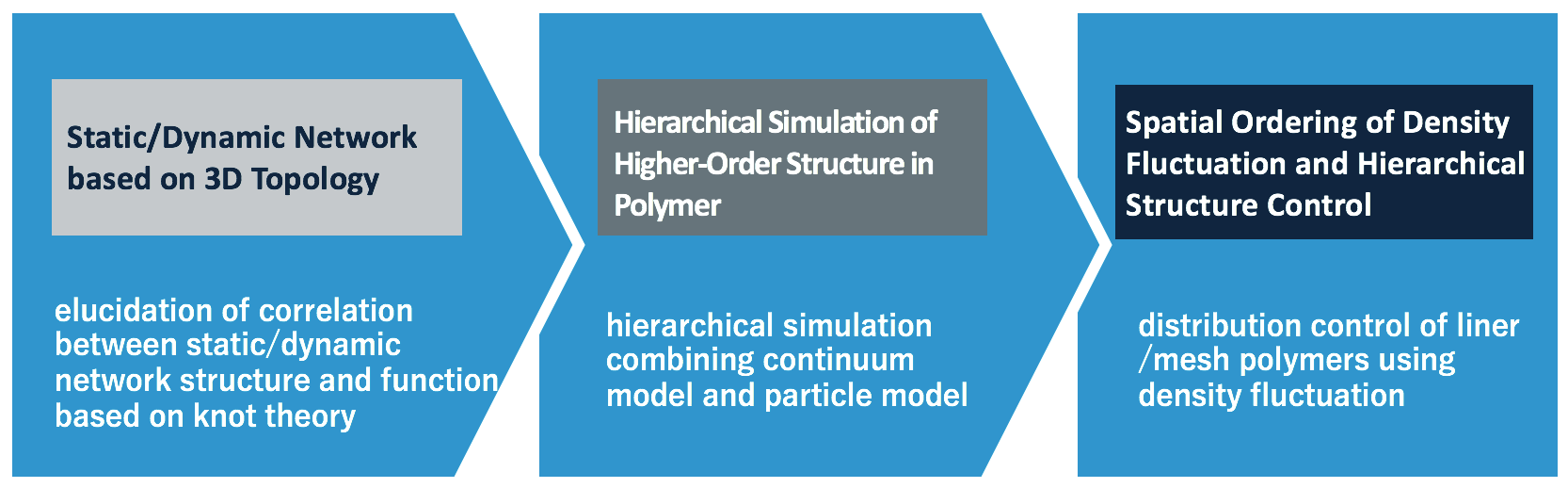
A02 Polymeric Materials using Network Analysis
| Members |
Koya Shimokawa (Saitama University) Takeshi Aoyagi (AIST) |
|---|---|
| Goal | Revealing the correlation between topological invariance derived from knot theory and materials property by describing homogeneous network polymer as a static network in 3D space. Predicting the dynamic network structure optimizing/controlling density fluctuation, and synthesizing multi-function polymers. |
| Materials | Multi-function Polymer |
| Mathematical Method | 3-D Topology |
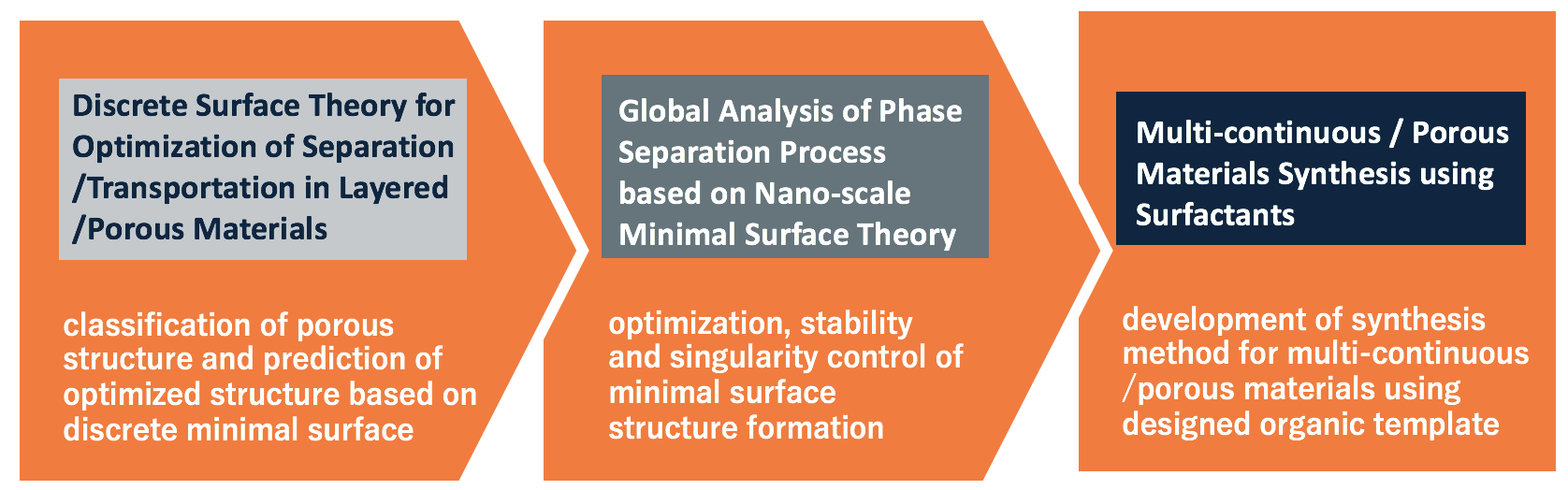
A03 Dynamic Structure Formation of Minimal Surfaces and Nano-structures
| Members |
Motoko Kotani (Tohoku University) Hisashi Naito (Nagoya University) Seiichi Takami (Nagoya University) |
|---|---|
| Goal | Classifying and optimizing multi-continuous porous structures based on discrete surface theory. Finding out a guiding principle for control of dynamic structure formation using global analysis. Realizing designed structures by phase separation through sophisticated interface control techniques. |
| Materials | Porous Materials (innovative catalysts, next generation batteries) |
| Mathematical Method | Discrete Minimal Surfaces |
B01 Information Science for Materials Science
| Members |
Takaaki Ohnishi (University of Tokyo) Akihisa Ichiki (Nagoya University) |
|---|---|
| Goal | Quantifying complex and hierarchical network in materials. Developing efficient and accurate methods for estimation of function of materials based on real-space imaging (topology of materials). Cooperating with A01-A03 taking advantage of these methods. |
| Method | Network Analysis, Image Analysis, Machine Learning |
Expected Achievements and Scientific Significance
In academia the structure-function-process correlation principle is deepening, and new phase materials are being created using the power of information science and data science. In mathematics discrete geometric analysis and discrete dynamical systems that understand complex and multiscale structures hierarchically and study the correlation of discrete and continuous are making great progress. These contribute to materials development and human resources development for the big data society.
Key Words
Discrete geometric analysis
The discrete form of geometric analysis analyzing macroscopic geometric structure is discrete geometric analysis. The relationship of discrete and continuous is understood by developing a technique to find the continuous structure behind the discrete data.
Data-driven materials design
If conventional materials development is the forward problem of finding functions from structure, aiming to use data analysis techniques to solve the inverse problem of finding structures that have the required functions is data-driven materials design. It is also called materials informatics.
